- Peserta didik dapat Menganalisis kaidah Pencacahan dan notasi faktorial (!)
Kaidah Pencacahan
Kaidah pencacahan atau dalam bahasa inggris disebut sebagai (Counting Rules) merupakan sebuah cara atau aturan untuk menghitung seluruh kemungkinan yang bisa terjadi dalam suatu percobaan tertentu.
Kaidah Pencacahan
Kaidah pencacahan merupakan sebuah aturan membilang untuk mengetahui banyaknya kejadian atau objek-objek tertentu yang muncul. Disebut sebagai pencacahan sebab hasilnya berwujud suatu bilangan cacah.
Adapun beberapa metode pada kaidah pencacahan antara lain yaitu: metode aturan pengisian tempat (Filling Slots), metode permutasi serta metode kombinasi. Berikut penjelasannya lebih lanjut.
Aturan Pengisian Tempat
Sebagai contoh ada suatu kasus di bawah ini:
Gilang memiliki 3 kaos dengan warna putih, merah dan biru dan juga memiliki 2 celana panjang yang berwarna hitam dan cokelat.
Tentukan beberapa kemungkinan Gilang akan menggunakan kaos dan juga celana panjang!
Penyelesaian:
Ada 3 cara untuk menentukan berbagai kemungkinan Gilang menggunakan kaos dan celana panjang.
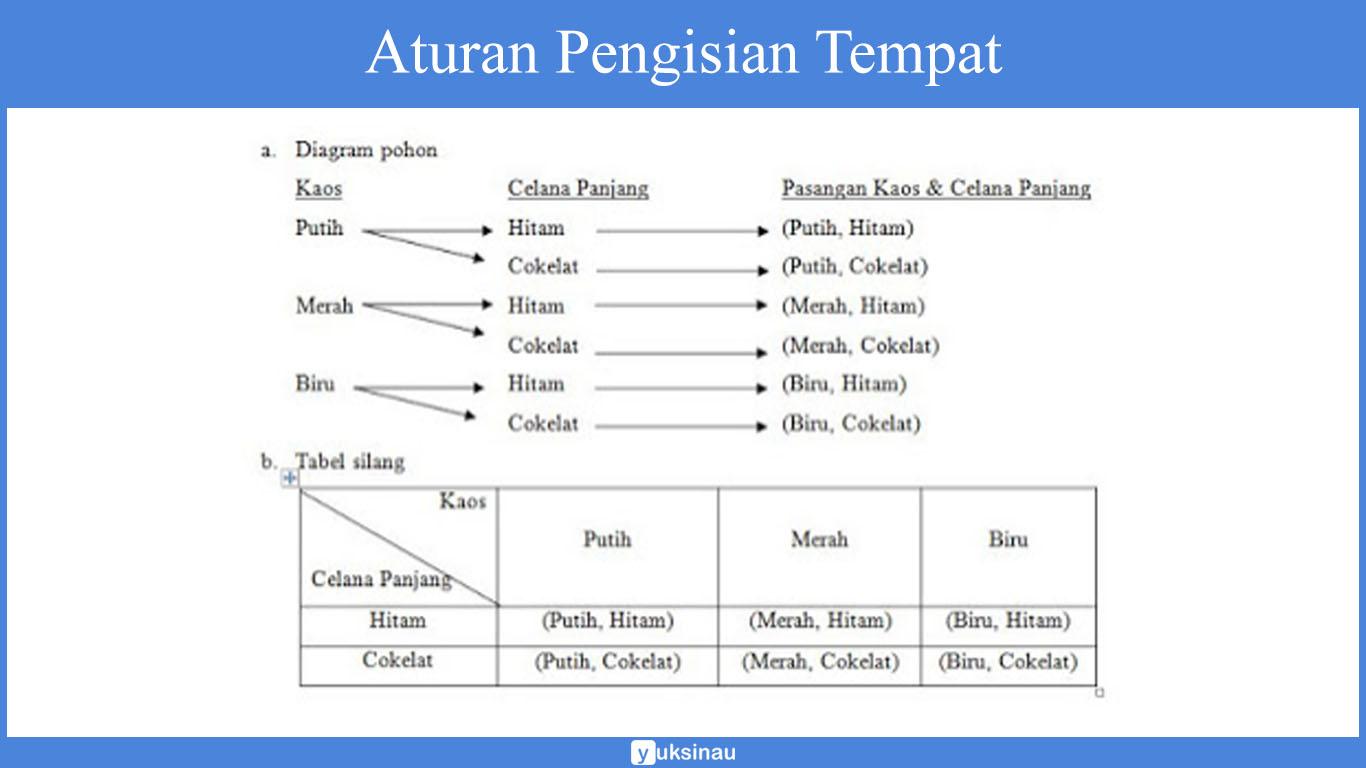
c. Himpunan pasangan terurut
{(Putih, Hitam), (Putih, Cokelat), (Merah, Hitam), (Merah, Cokelat), (Biru, Hitam), (Biru, Cokelat)}
Dari ketiga metode atau cara di atas, bisa kita simpulkan bahwa banyaknya cara Gilang memakai kaos dan juga celana panjang ada sebanyak 6 cara = 3 × 2 = banyak cara menggunakan kaos × banyak cara menggunakan celana
panjang.
panjang.
Aturan Perkalian
Apabila sebuah kejadian bisa berlangsung dalam n tahap yang saling berurutan di mana tahap 1 bisa berlangsung dalam q1 cara, tahap 2 bisa berlangsung dalam q2 cara, tahap 3 dapat terjadi dalam q3 cara demikian seterusnya hingga tahapan ke – n bisa berlangunsg dalam qncara maka kejadian tersebut bisa terjadi secara berurutan dalam q1 × q2 × q3 × … × qn dengan cara berbeda.
Sebagai contoh:
Berapa banyaknya cara atau metode untuk memilih 3 pengurus OSIS yang terdiri atas ketua, sekretaris serta bendahara dari total 8 orang siswa?
Penyelesaian:
Misal ada 3 tempat untuk mengisi posisi ketua, sekretaris dan bendahara yang kita visualkan seperti di bawah ini:
Ketua Sekretaris Bendahara
Dari ke-8 siswa itu, seluruh berhak dipilih untuk menjadi ketua sehingga terdapat 8 cara untuk mengisi posisi ketua.
Sebab 1 orang telah menjadi ketua maka tinggal 7 orang yang berhak untuk dipilih menjadi sekretaris sehingga terdapat 7 cara untuk mengisi posisi sekretaris.
Sebab 1 orang telah terpilih menjadi ketua serta 1 orang sudah menjadi sekretaris maka tinggal 6 orang yang berhak untuk dipilih menjadi bendahara sehingga terdapat 6 cara untuk mengisi bendahara.
Ilustrasi seperti tabel di bawah ini:
| 8 | 7 | 6 |
Ketua Sekretaris Bendahara
Banyak cara untuk memilih 3 pengurus OSIS tersebut yaitu 8 × 7 × 6 = 336
Aturan Penjumlahan
Sebagai contoh ada sebuah kejadian yang bisa terjadi dalam n cara yang berlainan (saling asing) di mana dalam cara pertama ada p1kemungkinan hasil yang berbeda.
Pada cara kedua ada p2 kemungkinan hasil yang berbeda. Pada cara ketiga ada p3kemungkinan hasil yang berbeda.
Serta demikian selanjutnya hingga cara yang ke – n ada pnkemungkinan hasil yang berbeda. Sehingga total banyak kemungkinan kejadian dalam peristiwa tersebut yaitu p1 + p2 + p3 + … + pn dengan cara berbeda.
Sebagai contoh:
Putra seorang pelajar SMK swasta di Purwokerto. Putra memiliki tiga jenis alat transportasi yang ia kendarai dari rumah ke sekolah. Antara laing: sepeda (sepeda mini, sepeda gunung), sepeda motor (yamaha, honda, suzuki) serta mobil (sedan, kijang, pick-up).
Pertanyaannya, berapa banyak cara Putra untuk berangkat dari rumah ke sekolah?
Penyelesaian:
Alat transportasi yang dipakai oleh Putra dari rumah ke sekolah hanyalah salah satu saja yakni sepeda atau sepeda motor atau mobil.
Tidak mungkin Putra mengendarai lebih dari satu kendaraan dalam waktu bersamaan. Banyaknya cara Putra berangkat dari rumah ke sekolah merupakan banyak cara mengendarai sepeda + banyak cara mengenadari sepeda motor + banyak cara mengendarai mobil = 2 + 3 + 3 = 8 cara.
Notasi Faktorial
Contohnya n ∈ himpunan bilangan asli. Notasi n! (dibaca: n faktorial) diartikan sebagai hasil kali dari bilangan-bilangan asli secara berurutan dari n sampai 1.
Maka kita tulis:
n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1.
Diartikan sebagai 1! = 1 dan 0! = 1.
Sebagai contoh:
1. Tentukan nilai dari 5!.
Jawab:
5! = 5 × 4 × 3 × 2 × 1 = 120.
2. Tentukan nilai dari 2! + 3!.
Jawab:
2! + 3! = (2 × 1) + (3 × 2 × 1) = 2 × 6 = 12
Kerjakanlah soal latihan berikut ini!
1. Budi mempunyai koleksi 3 pasang sepatu dengan merk yang berbeda, dan 4 baju yang berlainan coraknya, serta 3 celana yang berbeda warna. Banyak cara berpakaian Budi dengan penampilan yang berbeda adalah ….
2. Empat siswa dan dua siswi akan duduk berdampingan. Apabila siswi selalu duduk paling pinggir, banyak cara mereka duduk adalah ….
3. Ana mempunyai baju merah,hijau, biru, dan ungu. Ana juga memiliki rok hitam, putih, dan coklat. Berapa banyak pasangan baju dan rok yang dapat dipakai Ana?
4. Terdapat angka 3, 4, 5, 6, 7yang hendak disusun menjadi suatu bilangan dengan tiga digit. Berapa banyak bilangan yang dapat disusun bila angka boleh berulang?
5. Dari angka-angka 0, 1, 2, 3, 4 akan dibentuk menjadi suatu bilangan yang terdiri dari empat angka. Berapa banyak bilangan yang dapat disusun jika:
5a. Angka boleh berulang?5b. Angka tidak boleh berulang?
6. Terdapat angka-angka 3, 4, 5, 6, 7, 8, 9 akan disusun menjadi bilangan genap yang terdiri dari empat digit dengan angka-angka yang tidak boleh berulang. Tentukan banyak bilangan genap yang dapat terbentuk dari angka-angka tersebut!
7. Tentukan Nilai dari : 6!
8. Nilai dari 3!.4! =...
9.
8!.2!4!
=..
10. (5! + 3!) - (4!.3!)=.....
Tidak ada komentar:
Posting Komentar