SETELAH MEMPELAJARI MATERI DAN MENGERJAKAN LATIHAN SERTA KEGIATAN DI BAB INI, SISWA DIHARAPKAN MAMPU:
1. MENENTUKAN JARAK ANTAR TITIK PADA BANGUN RUANG DIMENSI TIGA DENGAN BENAR
2. MENENTUKAN JARAK TITIK DAN GARIS PADA BANGUN RUANG DIMENSI TIGA SECARA CERMAT, SERTA
3. MENENTUKAN JARAK TITIK DAN BIDANG PADA BANGUN RUANG DIMENSI TIGA DENGAN TEPAT
Pengertian Bangun Ruang
Bangun ruang adalah bangun matematika yang mempunyai isi atau Volume. Bangun ruang sering juga disebut bangun 3 dimensi karena memiliki 3 komponen utama sebagai berikut.
Bagian-bagian bangun ruang :
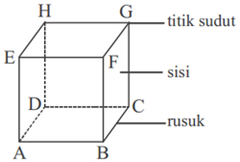
· Sisi :bidang pada bangun ruang yang membatasi antara bangun ruang denganruangansekitarnya
· Rusuk :pertemuan dua garis yang berupa ruas garis pada bangun ruang.
· Titik sudut :titik hasil pertemuan rusuk yang berjumlah tiga atau lebih.
- Diagonal Ruang : adalah suatu bangun ruang adalah ruas garis yang menghubungkan dua titik berhadapan pada bangun ruang tersebut
Diagonal sisi : adalah ruas garis yang menghubungkan dua titik berhadapan pada sisi tersebut
Bidang Diagonal : Bidang yang menghubungkan rusuk-rusuk yang berhadapan, sejajar dan tidak terletak pada bidang suatu bangun atau bidang yang melalui diagonal alas dan rusuk tegak
Jenis-Jenis Bangun Ruang yang umum dikenal adalah:
1. Kubus
2. Balok
3. Prisma
4. Limas
5. Kerucut
6. Tabung
7. Bola
A. KUBUS
Disebut bangun ruang kubus ketika bangun tersebut dibatasi oleh 6 buah sisi yang berbentuk persegi (bujur sangkar). Bangun ruang ini mempunyai 6 buah sisi, 12 buah rusuk, dan 8 buah titik sudut. Beberapa orang sering menyebut bangun ini sebagai bidang enam beraturan dan juga prisma segiempat dengan tinggi sama dengan sisi alas.
Bagian-bagian Kubus
TIga bagian utama dalam bangun ruang kubus adalah sisi, rusuk, dan titik sudut. Selain itu masih ada yang disebut dengan diagonal bidang dan diagonal ruang. Perhatikan gambar kubus di bawah ini.
Kubus ABCD.EFGH dibatasi oleh bidang ABCD, ABFE, BCGF, CDHG, ADHE, dan EFGH. Bidang-bidang tersebut disebut sisi-sisi kubus ABCD.EFGH. Selanjutnya, AB , BC , CD , AD , EF , FG , GH , EH , AE , BF , CG , dan DH disebut rusuk-rusuk kubus.
Berikut jumlah bagian-bagian kubus
1. Titik sudut 8 buah
2. Sisi berjumlah 6 buah (luasnya sama)
3. Rusuk berjumlah 12 buah sama panjang
4. Diagonal bidang berjumlah 12 buah
5. Diagonal ruang berjumlah 4 buah.
6. Bidang diagonal berjumlah 6 buah
Silahkan sobat coba cari sendiri ya mana-mana bagian kubus di atas sambil dicocokan jumlahnya.
Rumus-rumus Kubus
Volume = s x s x s = s3
Luas Permukaan = 6 s x s = 6 s2
Panjang Diagonal Bidang = s√2
Panjang Diagonal Ruang = s√3
Luas Bidang Diagonal = s2√2
keterangan:
s = panjang sisi kubus
B. BALOK
Coba kalian perhatikan benda-benda di sekitar kalian, banyak sekali sebenarnya benda yang memiliki bentuk bangun ruang balok. Kardus mie instan favorit kalian bentuknya adalah balok, kulkas di dapur rumah juga berbentuk balok. Lantas kenapa benda-benda tersebut dinamakan balok?
Apa itu balok?
Balok adalah bangun ruang yang memiliki tiga pasang sisi segi empat (total 6 buah) dimana sisi-sisi yang berhadapan memiliki bentuk dan ukuran yang sama. Berbeda dengan kubus yang semua sisinya berbentuk persegi yang sama besar, balok sisi yang sama besar hanya sisi yang berhadapan dan tidak semuanya berbentuk persegi, kebanyakan bentuknya persegi panjang. Buat lebih memahami silahkan sobat amati lagi kulkas di bawah ini.
Bagian-bagian Balok
Bagian-bagian dari bagung ruang sisi datar ini sama seperti bagian-baian kubus. Sebuah balok terdiri dari sisi, sudut, diagonal bidang, diagonal ruang, dan yang terakhir adalah bidang diagonal. Berikut rincian jumlahnya
1. Titik sudut 8 buah
2. Sisi berjumlah 6 buah (luasnya beda-beda)
3. Rusuk berjumlah 12 buah
4. Diagonal bidang berjumlah 12 buah
5. Diagonal ruang berjumlah 4 buah.
6. Bidang diagonal berjumlah 6 buah
Rumus-rumus Balok
Volume = panjang x lebar x tinggi = p x l x t
Luas Permukaan = 2 (pl + pt + lt)
Panjang Diagonal Bidang = √(p2+l2) atau √(p2+t2) atau √(l2+t2)
Panjang Diagonal Ruang = √(p2+l2+t2)
Luas Bidang Diagonal = tergantung dari bidang diagonal yang mana
Keterangan:
p = panjang
l = lebar
t = tingi
C. LIMAS
Bagun ruang sisi datar berikutnya adalah limas. Pernahkah kalian melihat piramid yang ada di mesir? Nah, piramid tersebut memiliki bentuk bangun ruang limas.
Apa itu Limas?
Limas adalah bangun ruang dengan alas berbentuk segi banyak, bisa segi tiga, segi empat, segi lima, dll dan bidang sisi tegaknya berbentuk segitiga yang berpotongan pada satu titik puncak. Ada banyak macam bangun ruang limas. Penamaannya berdasarkan bentuk alasnya.
| Limas Segitiga Beraturan |  |
| Limas Segiempat Beraturan |  |
| Limas Segitiga Sembarang |  |
| Limas Segiempat Sembarang |  |
Bagian-bagian Limas
Sebuah limas terdiri dari sisi alas, sisi tegak, rusuk, titik puncak, dan tinggi. Jumlah sisi tegak akan sama dengan jumlah sisi alas. Jika alasnya segitiga maka jumlah sisi tegaknya adalah 3, jika alasnya berbentuk segilima maka jumlah sisi tegaknya adalah 5. Jumlah rusuknyapun mengikuti bentuk alas. Jika alasnya segitiga maka jumlah rusuknya 6, jika alasnya segiempat maka jumlah rusuknya 8, pokoknya 2 kalinya.
Sebuah limas pasti akan memiliki puncak dan tinggi. Tinggi limas adalah jarak terpendek dari puncak limas ke sisi alas. Tinggi limas selalu teka lurus dengan titik potong sumbu simetri bidang alas.
Rumus rumus Limas
Volume Limas = 1/3 Luas Alas x Tinggi
Luas Permukaan = Jumlah Luas Alas + Jumlah Luas sisi tegak
D. PRISMA
Apa itu Prisma?
Perhatikan gambar bangun ruang sisi datar di atas. Gambar tersebut menujukkan beberapa contoh dari bangun ruang prisma.Bangun-bangun tersebut memiliki bidang alas dan bidang atas yang sejajar dan kngruen. Sisi linnya berupa sisi tegak berbentuk jajargenjang atau pesegi panjang yang tegak lurus ataupun titik dengan bidan alas dan bidang atasnya. Itulah kurang lebih definisi prisma.
Jika dilihat lagi dari rusuk tegaknya, prisma dapat dibedakan menjadi dua, yakni prisma tegak dan prisma miring. Prisma tegak adalah prima yang rusuk-rusuknya tegak lurus dengan bidang lasa dan bidang atas. Prisma miring adalah prisma yang rusuk-rusuk tegaknya tidak tegak lurus pada bidang atas dan bidang alas.
Jika dilhat dari bentuk alasnya aada yang namanya prisma segitiga, prisma segi emapat, prisma segi lima, dan seterusnya. Jika alasnya berbentuk segi n sobat bisa memberikan nama prisma segi n.
Bagian-Bagian Prima
Sebuah bangun ruang sisi datar yang bernama prisma terdiri dari alas dan sisi atas yang sama dang kongruen, sisi tegak, titik sudut, dan tinggi. Tinggi prisma adalah jarak antara bidang alas dan bidang atas. Sobat bisa amati gambar berikut:
Rumus Prisma
Volume = Luas alas x Tinggi
Luas permukaan = (2 x Luas Alas) + (Keliling alas x tinggi)
Luas permukaan = (2 x Luas Alas) + (Keliling alas x tinggi)
E) Kerucut
Merupakan bangun yang dibatasi oleh alas yang berbentuk lingkaran dan selimut yang berbentuk lengkung
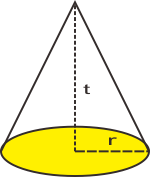
Ciri-ciri KERUCUT,antara lain:
Ø Kerucut merupakan bangun ruang berbentuk limas yang alasnya berupa lingkaran,
Ø Kerucut mempunyai 2 sisi,
Ø Kerucut tidak mempunyai rusuk,
Ø Kerucut mempunyai 1 titik sudut,
Ø Jaring-jaring kerucut terdiri dari lingkaran dan segi tiga.
Rumus Luas Kerucut
L = π r2 + π dxt
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi kerucut
Rumus Volume Kerucut
V = 1/3 ( π r2 x t )
V : volume
r : jari-jari lingkaran alas
t : tinggi kerucut
F) Tabung
Merupakan bangun yang dibatasi oleh sisi lengkung dan buah lingkaran
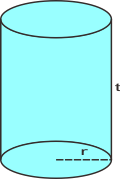
Ciri-ciri TABUNG, antara lain:
Ø Tabung merupakan bangun ruang berupa prisma tegak dengan bidang alas dan atas berupa lingkaran,
Ø Tinggi tabung adalah jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas,
Ø Bidang tegak tabung berupa lengkungan yang disebut selimut tabung,
Ø Jaring-jaring tabung tabung berupa 2 buah lingkaran dan 1 persegi panjang.
Rumus Luas Permukaan Tabung
L = 2 x ( π r2 ) + π d x t
L : luas permukaan
r : jari-jari lingkaran alas
d : diameter lingkaran alas
t : tinggi tabung
Rumus Volume Tabung
V = 1/3 (luas alas x t)
V : Volume
luas alas : π r2
r :jari-jari alas
t : tinggi tabung
t : tinggi tabung
G) Bola
Merupakan bangun yang dibatasi oleh sisi lengkung
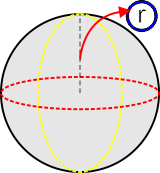
Ciri-ciri BOLA, antara lain:
Ø Bola merupakan bangun ruang berbentuk setengah lingkaran diputar mengelilingi garis tengahnya,
Ø Bola mempunyai 1 sisi dan 1 titik pusat,
Ø Sisi bola disebut dinding bola,
Ø Bola tidak mempunyai titik sudut dan rusuk,
Ø Jarak dinding ke titik pusat bola disebut jari-jari,
Ø Jarak dinding ke dinding dan melewati titik pusat disebut diameter.
Rumus Luas Permukaan Bola
L = 4 π r2
L : luas permukaan
r : jari-jari bola
Rumus Volume Bola
V = 4/3 π r3
V : volume
r : jari-jari bola
SELESAIKANLAH SOAL BERIKUT INI, TUGAS DIKUMPULKAN PALING LAMBAT 31 JULI 2019 PUKUL 24.00 WIB
SOAL LATIHAN 1
1. Sebuah kubus memiliki panjang rusuk 12 cm. Tentukan Luas dan volume kubus itu!
2. Panjang semua rusuk kubus 240 cm. Hitunglah volume kubus tersebut (dalam cm).
3. Diketahui luas permukaan sebuah kotak berbentuk kubus 96 cm2. Hitunglah volume kotak tersebut!
4. Andi akan mengirim paket berupa 125 souvenir yang dikemas dalam kotak berbentuk kubus berukuran 4 cm. Sebelum dikirim, souvenir tesebut dimasukan kedalam kardus besar yang berbentuk kubus hingga kardus terisi penuh. Berapakah ukuran panjang kotak kardus yang digunakan Andi?
5. Kamar mandi Wira memiliki bak berbentuk kubus dengan kedalaman 1 meter. Bak tersebut diisi air hingga penuh. Berapa liter air yang mengisi bak mandi Wira?
6. Sebuah aquarium berbentuk kubus memiliki volume 343 liter. Berapa cm tinggi aquarim tersebut?
7. Di ketahui ada sebuah balok memiliki panjang 9 cm , lebar 7 cm , dan tinggi nya 3 cm , maka carilah berapa luas permukaan dan volume dari balok tersebut ?
8. Bangun ruang sebuah balok telah di ketahui luas nya 128 cm. Lalu hitunglah volume balok itu jika tinggi nya yakni 4 cm ?
9. Sebuah mainan berbentuk balok volumenya 140 cm3. Jika panjang mainan 7 cm dan tinggi mainan 5 cm, tentukan lebar mainan tersebut!
10.Volume sebuah balok 120 cm3. Jika panjang balok 6 cm dan lebar balok 5 cm, tentukan tinggi balok tersebut.
11. Badu memiliki bak berbentuk balok dengan tinggi 50 cm, lebarnya 70 cm dan panjang 90 cm. Bak tersebut akan diisi air. Berapa banyak air yang dibutuhkan untuk mengisi 2/3 bagian bak milik badu?





Tidak ada komentar:
Posting Komentar